Zgodba o kvadraturi kroga nastaja že več kot 4000 let. Kvadratura kroga je znan problem klasične geometrije, ki zahteva, da z ravnilom in šestilom konstruiramo stranico kvadrata, ki ima enako ploščino kot dani krog. Če sta ploščini kvadrata s stranico a in kroga s polmerom r enaki, mora veljati: a=r√π. Če je r = 1, je a =√π.

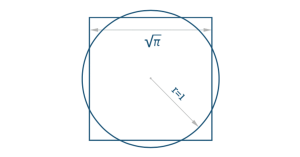
Danes vemo, da konstrukcija dolžine √π s šestilom in ravnilom v ravnini ni izvedljiva. No, tako prepričanje velja med ljudmi. Natančna rešitev kvadrature kroga naj torej ne bi obstajala, obstaja pa veliko dobrih in tudi zanimivih približkov. Izraz kvadratura kroga se danes uporablja v vsakdanjem jeziku in pomeni, da se ukvarjamo s problemom, ki nima rešitve. 

Kot bomo videli, pa ta izraz ni najbolj primeren. Vemo, da živimo v vesolju, v katerem je končno mnogo delcev. Vse, kar nastane v našem vesolju, se mora zaokrožiti. Zato se lahko vprašamo, kako dober približek zares potrebujemo. Ljudje smo pri tem bolj ali manj iznajdljivi. Tako recimo praznujemo 14. marca kot dan števila π. Morda bi bilo bolj smiselno, če bi ga praznovali 22. julija, saj je 22/7 veliko natančnejši približek števila π, kot je 3,14.

Poglejmo, kako so ta problem s približki rešili staroegipčanski matematiki. Enega od zanimivih približkov za π najdemo v Rhindovem papirusu, ki je starejši od 3600 let. Napisal naj bi ga pisar Ahmos, v njem pa odkrijemo, kaj vse so poznali že staroegipčanski matematiki.

Lahko si zamislimo problem, ki so ga imeli Egipčani. Če so žito spravljali v okrogle silose, so morali izračunati tudi njihov volumen. Zato so morali izračunati ploščino kroga, ki je bil osnovna plošča silosa. Takole nalogo lahko najdemo na Rhindovem papirusu: izračunaj prostornino valjastega silosa za žito s premerom 9 komolcev in višino 10 komolcev. Rezultat izrazi v kubičnih komolcih. 

In kakšno rešitev so zapisali že pred 4000 leti? Takole je zapisano: od premera kroga odštej eno devetino in dobiš dolžino stranice kvadrata. Poglejmo sliko približka kvadrature kroga. Slika predstavlja zelo dober približek, saj sta ploščini kvadrata in kroga skoraj popolnoma enaki. 

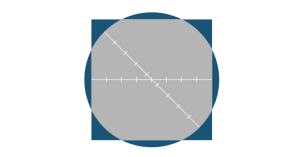
Če je premer kroga devet enot, se za stranico kvadrata uporabi osem enot.

Prostornina V = a² · h = 8 · 8 · 10 = 640 

Površina kroga je π · r². Površino kvadrata so izračunali kot (2 · r · 8/9)². Ko so od premera odšteli eno devetino, so dobili dolžino stranice kvadrata. Za π so torej uporabili približek 4 · 64/81, kar je enako 256/81 oziroma približno 3,16. 

Staroegipčanski matematiki so pred 4000 leti poznali dokaj dober približek, ki je po eni strani zelo preprost, po drugi strani pa tudi v praksi zelo uporaben. Ljudje se torej že več kot 4000 let uspešno spopadamo s približki. Na Rhindovem papirusu se najde rešitev še za marsikateri problem. Vidimo, da je tudi Pitagora imel dobre učitelje.

Problem kvadrature kroga je reševal tudi Leonardo. Čeprav njegovo delo ni ohranjeno, pa lahko ugibam, do kakšnih rezultatov je prišel. Vem, da se je Leonardo zavedal, da problema kvadrature kroga ne bo mogel točno razrešiti v dveh dimenzijah, zato je pri svojem razmišljanju zašel še v tretjo dimenzijo. Zanimivo, kajne? Rešitev se včasih najde, ko dodamo še eno dimenzijo. Leonardo si je zamislil, da bi do rešitve lahko prišel z valjem. Če je višina valja točno polovico polmera kroga, ki je osnovna ploskev valja, potem ima plašč valja enako površino kakor osnovna ploskev valja, torej krog. Plašč valja ima enako površino kakor krog, če pa plašč valja raztegnemo, dobimo pravokotnik. Stranici pravokotnika imata dolžini 2πr in r/2. Površina pravokotnika je torej πr².

Leonardo je poskušal rešiti problem kvadrature kroga tako, da je uporabil še tretjo dimenzijo. Morda je njegovo delo nekje zastalo, ker pri tej rešitvi ni jasno, kaj pomeni, da se plašč valja raztegne v pravokotnik. Matematika zahteva popolno natančnost. Po navedenem postopku lahko torej konstruiramo krog in pravokotnik, ki imata enako površino. Lahko se izvede tudi kvadratura pravokotnika. Ostane majhen problem, ki se skriva v izravnavi plašča. Morda lahko valj kar zakotalimo in označimo površino, ki jo določa plašč valja?

Potem pa je leta 1914 Ramanujan izdelal konstrukcijo kvadrature kroga z natančnostjo na devet mest. Ramanujan se je ukvarjal z neskončnimi vrstami in je odkril tudi odlične približke za število π. Pri konstrukciji kvadrata je upošteval, da mora biti stranica kvadrata za faktor √π daljša od polmera kroga. Potem je z danim polmerom moral konstruirati stranico kvadrata. Pri tej konstrukciji se za vrednost π upošteva vrednost, ki se s pravo vrednostjo π ujema na prvih osmih decimalnih mestih. Če za π upoštevamo deset decimalnih mest, dobimo: π = 3,1415926536. Ramanujan je upošteval naslednjo vrednost za π:

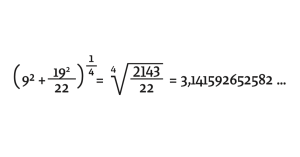Ramanujan je navedeni približek za število π in število √π izdelal samo z ravnilom in šestilom. Konstrukcija, ki ustreza prikazani vrednosti π, je prikazana na sliki. Če je polmer kroga OC enak enoti 1, potem je približek za π enak trikratni dolžini OC. Stranica kvadrata je približek za √π.

Ocena natančnosti konstrukcije je naslednja: če je premer kroga dolg en kilometer, bo napaka pri dolžini stranice kvadrata manjša od 0,01 milimetra.

Lahko se začudimo: Ramanujanu je uspelo približek za število √π konstruirati samo z ravnilom in šestilom. Napaka pri dolžini stranice kvadrata na sliki je manjša od 0,000001 milimetra. To je tako majhna napaka, da je s prostim očesom ne moremo zaznati.

Na tem mestu pa nas čaka novo presenečenje. Če imata krog in kvadrat enako površino, pa je obseg kvadrata večji od obsega kroga. Obseg kvadrata je namreč 4√πr, obseg kroga pa 2πr. Stoodstotna natančnost zahteva, da imajo črte, ki označujejo stranice kvadrata, in krožnica, ki določa krog, samo eno dimenzijo. Če imajo tako črte kot krožnica tudi debelino, se zgodi nekaj nepričakovanega. 

Z debelino črte se površina kvadrata povečuje hitreje kakor površina kroga.

Če upoštevamo notranji rob črt kvadrata in krožnice, bi bila ploščina kroga za malenkost večja, če pa upoštevamo zunanji rob črt kvadrata in krožnice, je že ploščina kvadrata malo večja od ploščine kroga. Nekje okrog sredine črt kvadrata in krožnice obstaja tista popolna kvadratura kroga. Lahko samo ugotovim, da je debelina črt in krožnice na sliki malo predebela.

Lahko se podam v svoj domišljijski svet, v matematično vesolje, in si predstavljam krožnico in stranice kvadrata, ki so črte v pravem pomenu besede, torej brez debeline. Skrivajo se nekje znotraj narisane krožnice in stranic narisanega kvadrata. Ker imajo debelino nič, so našim očem nevidne. Predstavljam si jih lahko samo v svojem domišljijskem svetu. 

V svojem domišljijskem svetu si lahko predstavljam popolno kvadraturo kroga.

V domišljijskem svetu obstajajo črte in krožnice, ki nimajo debeline. Obstaja popolna natančnost. V domišljijskem svetu in matematičnem vesolju torej obstaja popolna kvadratura kroga. 

V našem svetu se spopadamo s približki. Največkrat se zadovoljimo s približki, ki so natančni na dve ali tri decimalna mesta. V tem primeru govorimo o približku, ki je pravilen na osem decimalnih mest. Če bi nam uspelo narediti dovolj tanko črto, bi lahko izdelali skoraj popolno kvadraturo kroga. Zdi se mi, da izraza kvadratura kroga ni ravno primerno uporabljati za probleme, ki nimajo rešitve. Če še enkrat pogledam zgornjo sliko, mi matematiko predstavi kot pravo umetnost. Če bi na sliki ostale le črte in krivulje, bi se prikazala prava umetnina z globokim sporočilom: kvadratura kroga. Vidim, kakšne možnosti obstajajo v našem svetu, ki je sestavljen iz končnega števila delcev. 

Odlomek je iz knjige Teorija vsega – Einsteinov trikotnik in dve vesolji, avtor Darko Šifrer. V knjigi si lahko preberete več o kvadraturi kroga, Ramanujanu, posebnemu številu π, Arhimedu in neskončnosti, o obliki vesolja in Einsteinovem trikotniku.